1、前言

金属中氢的捕获状态和氢脆之间有着密切关系。例如，冷拔珠光体钢已表明，尽管氢含量低，但在室温扩散的氢的弱捕获状态造成断裂应变显著下降。相反，尽管氢含量高，但在室温不扩散氢的强捕获状态对氢脆无害。弱捕获状态的捕获点是位错，空位，晶界，渗碳体界面和晶格中的固溶体氢。然而，对于捕获点的影响和它们是如何造成氢脆的，人们却没有多少共识。对于Inconel 625和纯铁，人们检查了在室温扩散的弱捕获氢或固溶体氢的作用。结果显示，在充氢试样中有氢时，塑性应变会显著地增加晶格缺陷。由于这种晶格缺陷在后来的200℃退火时可去除，所以，有氢的应变过程造成的绝大多数缺陷不是位错，而是空位和空位团。此外，即使氢在断裂的最后阶段不存在，但当试样中仍有应变和弱捕获的扩散氢引起的晶格缺陷密度变大，韧性损失不会恢复。应当注意，在最后的断裂阶段，氢并不是必要条件。这些结果说明，应变和弱捕获的扩散氢造成晶格缺陷密度的增加，如空位和空位团是造成氢脆裂的直接因素。在没有氢的塑性变形中空位的生成是位错动力学的结果，如螺旋位错的交截或切削，或位于相距一段距离的滑移面和原子面上具有相反特性的刃型位错的组合。由于氢对空位具有稳定作用，在有氢存在的情况下，在塑性变形过程中可促使空位的形成。因此，对氢增强的应变引发的空位来说，氢和位错之间的相互作用是相当重要的。产生氢和位错之间的相互作用的方式有多种。由于位错四周形成的氢气氛的有效半径约为0.5nm，氢是从芯部到位于离芯部有一定点距离的位错的弹性场捕获的。以前有报道谈过，在各种金属的应力变形过程中有氚（超重氢）的解吸，这说明它是由运动位错传输的。此外，使用银装饰技术揭示在纯铝表面上滑移线有Ag(CN)2沉积，说明有氢的快速传输和这种位错。使用氢原子微印技术也获得了类似的结果：在Al-5%Mg合金表面的滑移线上观察到了银颗粒，这可能是由于运动位错把氢传输到表面造成的。在拉伸变形过程中检测到了从各种金属中解吸出来的氢，并在断裂时观察到有氢解吸峰值。虽然有许多文献报导说变形促使氢解吸，但是，有关塑性/弹性变形过程中各种金属的氢解吸的现场研究的详细文献却很少。

 

 

2、试验

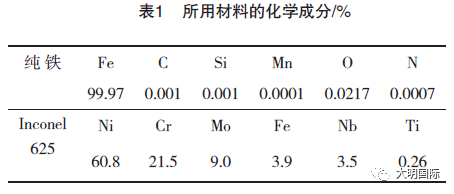
试验材料采用的是体心立方晶格的纯铁和面心立方晶格的镍基合金Inconel 625。表1所示为化学成分。为了在拉伸试验过程中施加张力，使用的是扁平试样，试样尺寸为1mm厚，20mm标准长和2.5mm宽。纯铁在氩气氛中以900℃退火0.5小时，然后进行炉内冷却，Inconel 625在氩气氛中以1150℃进行固溶处理1.5小时，然后进行水淬处理。用砂纸对所有热处理试样的表面进行抛光，去除残余的氧化膜。使用电流密度为50A/m2的恒流器，通过阴极电解法进行充氢处理，为了使试样的氢饱和，充氢时间要足够长。除了标准部分，试样要用绝缘树脂包覆。试样用作工作电极，铂用作计量电极。使用的溶液为H2SO4，pH值为2.5，在水溶液中加入了0.09%的NH4SCN。纯铁用电解液的温度为30℃，Inconel 625用电解液的温度为90℃。充氢处理后，纯铁和Inconel 625的氢含量分别为1.3ppm和87ppm。使用慢应变速率技术，在安装有螺旋泵、涡轮分子泵，四极质谱仪（QMS）、真空计和焙烧加热器的真空室内分析了拉伸变形过程中氢解吸行为。在断裂或循环弹性应力之前，无论是经过充氢处理还是没有经过充氢处理的试样都承受拉伸应力。在室温条件下，当应变速率在4.2×10－6和4.2×10－3之间时，在真空室内利用四极质谱仪（QMS）观察到拉伸变形过程中试样的氢解吸（M/z = 2）和水解吸（M/z = 18）。分析是在充氢后约20分钟，当室内的真空压力为5.0×10－4Pa时开始的。由于人们认为在水中进行充氢处理会使吸收的水量增加，造成表面不平，所以，在分析前，利用砂纸对充氢表面进行了抛光处理。为了测量在变形过程中解吸氢的总量，在恒定加热速度为100℃/h时，利用气相色谱仪进行了热解吸分析（TDA）。为了在5分钟的取样间隔标定氢含量，使用的是标准的氩气+50vol ppm的H2混合气体。

 

 

3、试验结果 

 

3.1减去从H2O释放出来的碎片氢 

 

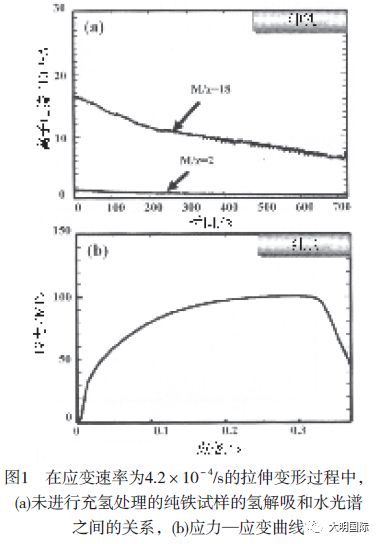
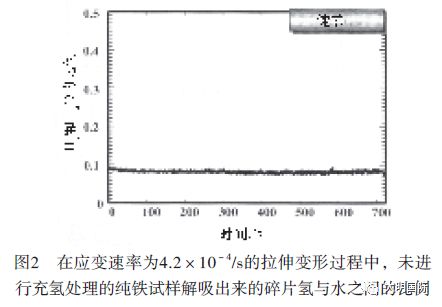
为了仅检测拉伸应力促使的氢解吸，必须要减去背景氢。由于在该试验中试样不进行加热，所以，试样表面解吸出来的氢和加热从真空室释出的氢的影响很小。但是，由于试样表面和/或真空室壁上吸收了大量的H2O，所以，不可低估碎片氢的影响。图1(a)和(b)所示为在900℃进行退火处理，并在断裂前承受应变速率为4.2×1－4/s的拉伸应力的未充氢处理的纯铁试样的氢解吸（M/z= 2）和水解吸（M/z = 18）光谱和相应的应力—应变曲线。虽然TDA发现未充氢试样的氢含量，但是，还是检测出了少量的氢，见图1（a）所示。这种氢解吸光谱不可能是试样中来的，可能是表面H2O中解吸出来的碎片氢。碎片氢解吸和水解吸数量之间的比例取决于所用QMS的种类，应该是恒定的。图2所示为在断裂前承受应变速率为4.2×10－4/s的拉伸应力的未充氢纯铁试样的比例。在断裂前的拉伸变形过程中，比例保持不变。因此，这不是试样内部氢的解吸光谱，而是H2O分离出来的碎片氢，所以必须作为背景氢予以扣除。对于未进行充氢处理的Inconel625试样来说，在断裂前的拉伸变形过程中，氢解吸和水解吸数量之间的比例也是恒定的。也要从下述的结果中减去背景氢。

 

 

 

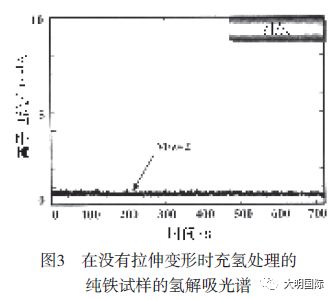
3.2　在没有拉伸变形时扩散的解吸氢

 

在真空室内，充氢处理的纯铁试样的氢解吸光谱不受拉伸应力的制约，如图3所示。在室温时，试样解吸出来的氢很少，也没有观察到有显著的氢解吸峰值。这是由于在室温下的热量使晶格内的氢原子扩散造成的氢解吸。为了仅仅区别拉伸应力促使的氢解吸，必须要减去没有拉伸应力时的扩散释放。Inconel 625的扩散释放产生的氢解吸与纯铁相似。要从下面给出的结果中减去没有拉伸应力的扩散释放。

 

 

3.3氢解吸量的确定取决于拉伸应力

 

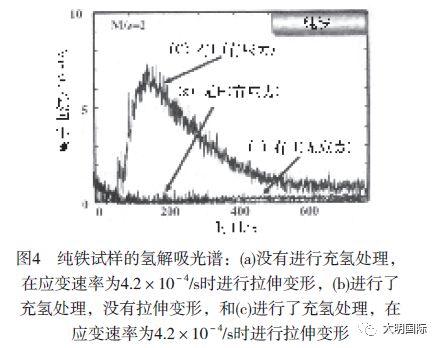
根据上面的第3.1和3.2节的讨论，要通过从氢解吸总量中减去下述两种氢来确定拉伸应力促使的氢解吸：（1）试样表面和/或真空室壁上H2O分离出来的碎片氢；（2）在室温时，当没有拉伸应力时分离出来的扩散氢。图4所示为(a)未进行充氢处理的纯铁试样在断裂前承受应变速率为4.2×10－4/s的拉伸应力时的氢解吸光谱，(b)在没有拉伸应力时充氢处理试样的氢解吸光谱，(c)进行充氢处理的纯铁试样在断裂前承受应变速率为4.2×10－4/s的拉伸应力时的氢解吸光谱。这是在氢解吸总量中扣除上述（1）和（2）的氢后的氢解吸光谱。在(a)和(b)的结果中，没有氢解吸光谱，说明已从氢解吸总量中扣除了（1）和（2）的背景氢解吸。这说明仅仅是从氢解吸总量中正确提取了拉伸应力促使的氢解吸。对于Inconel625来说，情况也是一样，仅仅是通过从氢解吸总量中扣除（1）和（2）来提取拉伸应力促使的氢解吸。

 

 

 

3.4塑性/弹性变形过程中的氢解吸行为

 

图5(a)所示为进行充氢处理的纯铁试样在断裂前承受应变速率为4.2×10－4/s的拉伸应力时的氢解吸光谱，图5(b)所示为其相应的应力—应变曲线。在弹性变形时，氢解吸少。相反，当塑性变形开始，应变超过屈服强度时，氢解吸迅速增加，达到最大值，然后，随着塑性应变的增加，逐渐降低。

 

 

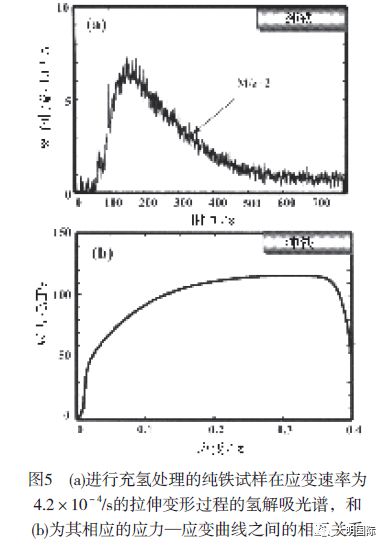
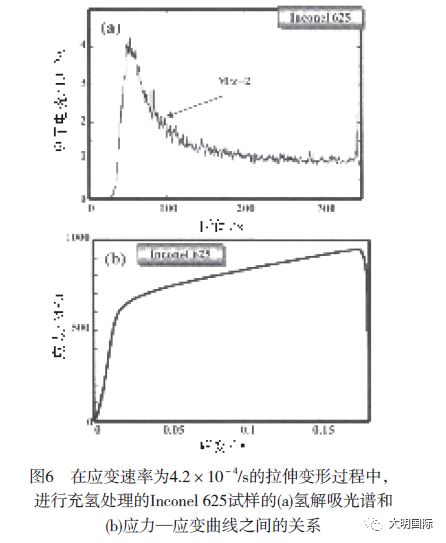
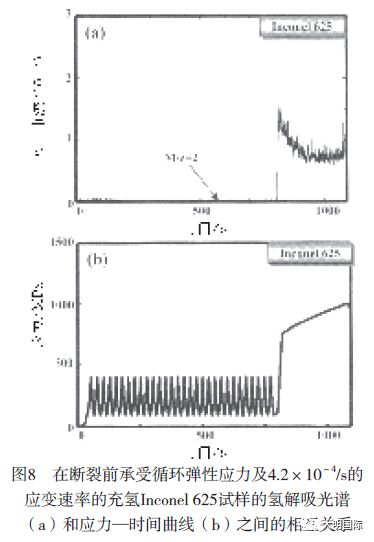
图6(a)所示为进行充氢处理的Inconel 625试样在断裂前承受应变速率为4.2×10－4/s的拉伸应力时的氢解吸光谱，图6(b)所示为其相应的应力—应变曲线。Inconel 625试样的氢解吸行为与纯铁试样的氢解吸行为相似。在弹性变形时，氢解吸很少。相反，当塑性变形开始，应变超过屈服强度时，氢解吸迅速增加，达到最大值，然后，随着塑性应变的增加，逐渐降低，在断裂时出现峰值。断裂时的峰值说明，这可能是当试样断裂时，断裂区域内累积的氢突然释放，然后出现一个新表面。在该试验中，当断裂后，氢解吸没有减少到零。这是由于在拉伸试验过程中试样的氢解吸造成真空压力发生变化或背景氢发生变化所致。在下面的结果中也观察到了断裂后的氢解吸，其原因大致相同。为了更加精确地检查塑性/弹性变形对氢解吸行为的影响，在断裂前，施加了循环弹性应力。图7(a)所示为进行充氢处理的纯铁试样在承受20～40MPa的30个弹性应力周期，然后在断裂前以4.2×10－4/s的应变速率施加拉伸应力时的氢解吸光谱，图7(b)所示为相应的应力时间曲线。在循环弹性应力条件下，氢解吸量小。当塑性变形开始, 应变超过屈服强度时, 氢解吸迅速增加, 达到最大值, 然后, 随着塑性应变的增加逐渐降低。图8(a)所示为进行充氢处理的Inconel 625试样在承受100～400MPa的30个弹性应力周期，然后在断裂前以4.2×10－4/s的应变速率施加拉伸应力时的氢解吸光谱，图8(b)所示为相应的应力时间曲线。在循环弹性应力条件下，氢解吸不增加。当塑性变形开始，应变超过屈服强度时，氢解吸迅速增加，达到最大值，随着塑性应变的增加，逐渐降低，然后，在断裂时达到峰值。

 

 

 

3.5氢解吸总量与应变速率的关系

 

如图9和10分别所示为承受4.2×10－5/s或4.2×10－3/s的应变速率的充氢试样的氢解吸光谱，也就是图5(a)和图6(a)中所用速率的10倍或十分之一。在所有的光谱中，氢解吸在塑性变形开始的屈服强度迅速增加，达到最大值，随着塑性应变的增加，逐渐降低。接着，比较了断裂前各种应变速率条件下的解吸氢总量。在产生断裂后，由于上面3.4节内所谈的背景氢的变化，氢解吸不能降至为零，所以，无法准确测量出解吸氢的总量。因此，通过使用氢的标准气体，利用TDA来精确地确定解吸氢的总量。

 

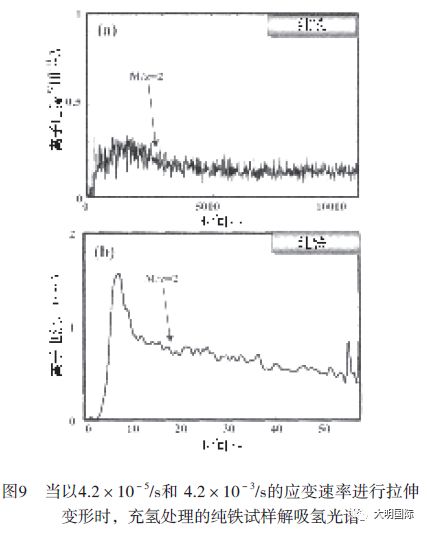
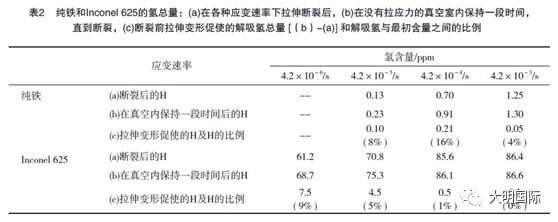
表2所示为利用TDA测量的纯铁和Inconel625的氢总量：(a)在各种应变速率下拉伸断裂后, (b)在没有拉应力的真空室内保持一段时间, 直到断裂, (c)断裂前拉伸变形促使的解吸氢总量 [(b)-(a)]和解吸氢与最初含量之间的比例。纯铁用的应变速率为4.2×10－5/s, 4.2×10－4/s和4.2×10－3/s，Inconel 625用的应变速率为4.2×10－6/s，4.2×10－5/s，4.2×10－4/s和4.2×10－3/s。表2中括号内的百分比为解吸氢与初始氢含量之间的比例。对于纯铁来说，当试样以4.2×10－4/s的应变速率进行变形时，拉伸应力促使的解吸氢的最大数量为0.21ppm，也就是初始氢含量的16%。相反，对于Inconel 625来说，拉伸应力促使的解吸氢总量是随着应变速率的降低而增加的，当试样以4.2×10－6/s的应变速率进行变形时，解吸氢总量为初始氢含量的9%。对于这两种试样来说，拉伸变形促使的解吸氢总量取决于应变速率。

 

 

 

4、讨论

 

4.1拉伸变形过程中促使氢解吸的因素

 

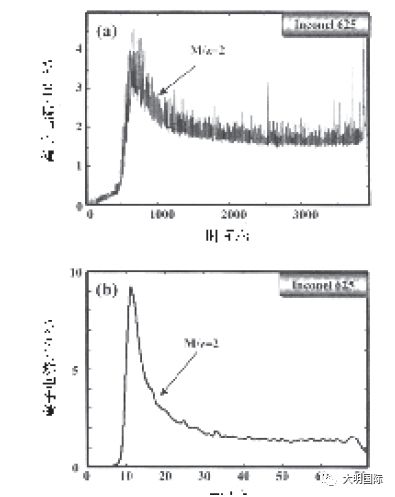
图10　当以（a）4.2×10－5/s和 （b）4.2×10－3/s的应变速率进行拉伸变形时，充氢处理的Inconel 625试样的解吸氢光谱

 

图5～10表明，根据拉伸变形前的氢解吸总量，氢离子密度（垂直轴）在拉伸变形后并没有移动到负的一侧（制约氢解吸），而是处于正的一侧（促使氢解吸）。这些结果说明即使在室温条件下拉伸应力也促使氢解吸。而且，在弹性变形条件下，氢解吸量小，然而当塑性变形开始时，它迅速增加。由于拉伸应力促使氢解吸的因素有下面五个：（A）变形过程中产生的热造成试样温度提高，（B）从试样表面上吸收的H2O释放出来的碎片氢，（C）试样表面上氧化物膜断裂，（D）变形形成的不平试样表面（使试样表面面积增大），（E）运动位错造成的氢输送。由于拉伸应力制约氢解吸的因素有下面两个：（F）塑性变形造成的氢捕获地点的增加，也就是说，晶格缺陷，（G）由于化学势降低致使氢的吸收能力增加。

 

首先，关于变形产生热造成试样温度提高的因素（A）可忽略不谈。这是因为对Inconel 625来说，虽然试样温度通常会随应变速率而增加，但解吸氢总量是随应变速率下降而增加的。拉伸测试过程中的实际试样表面温度测量表明，当应变速率为4.2×10－3/s时，断裂前它增加2℃，但是在应变速率为4.2×10－5/s时，没有检测到温度的变化。第二，关于从试样表面上的H2O中释放出来的碎片氢的因素（B）也可忽略不谈。这是因为虽然进行充氢和未进行充氢试样的表面条件相同，但在分析前，对未进行充氢试样进行了抛光处理，所以在图4（a）中的第一个试样上并没有观测到氢的解吸。第三，关于试样表面氧化膜断裂的因素（C）和关于变形造成试样表面不平（试样表面面积增大）的因素（D）对氢解吸的影响很小。是因为，虽然对所有的应变速率来说，已知的断裂应变几乎相同，但是由于氢解吸总量取决于应变速率。最后，位错的移动速度，也就是说，应变速率，可能与运动位错的氢传输有关。在表2内可看出解吸氢总量与应变速率之间的关系。因此，我们的结论是，关于运动位错造成氢传输的因素（E）是促使氢解吸的最有效的因素。

 

 

4.2运动位错造成的氢传输和应力—应变曲线之间的关系 

 

首先讨论一下在弹性变形过程中的氢解吸行为。如图6，8和10所示，在屈服强度高，弹性和塑性变形界限分明的Inconel 625的弹性变形过程中没有检测到氢解吸。这种行为说明，在Inconel625中没有位错移动，所以也没发生运动位错造成的氢传输。Inconel 625的化学势可能会由于弹性拉伸应力（因素G）而下降，这会限制氢解吸。相反，屈服强度低，没有明显的屈服点的纯铁在弹性变形过程中有轻微的氢解吸，见图5，7和9。这是因为尽管有弹性应力，但纯铁中不会发生位错阻塞，使滑移线上的可动位错与氢一起移动，并把氢传输到表面。

 

接着讨论一下塑性变形过程中的氢解吸行为。在这两种金属中，当塑性变形开始，应变超过屈服强度时，氢解吸迅速增加，达到最大值，然后随着塑性应变的增加逐渐降低。这说明塑性变形过程中的氢解吸与运动位错一致。恒定应变速率下运动位错传输的氢总量取决于位错四周氢的浓度和到达试样表面的运动位错的总量。运动位错四周的氢浓度由下式表达：

 

Cx＝CLexp(EB/kBT)…………………………（1）

 

式中，CX是捕获位置的原子比率计算的氢浓度，CL是固溶氢体的浓度，kB是波尔兹曼常数，T是绝对温度，EB是捕获位置和氢间的结合能。公式（1）表明，当初始氢浓度恒定时，位错四周氢的浓度取决于EB和T。由于本研究中的拉伸试验是在恒定温度进行的，位错四周的氢浓度仅仅取决于EB。一般来说，在体心立方晶格的α铁中，有静水应力场的刃型位错和氢之间的相互作用大，有报道称，刃型位错和氢之间的结合能为58kJ/mol。相反，没有静水压力场的螺旋位错和氢之间的相互作用要比刃型位错的相互作用小。有报道说，螺旋位错和氢之间的结合能为19 kJ/mol和20～30kJ/mol。虽然研究人员所取得的结合能的值大小有区别，但对于刃型位错和氢之间的结合能要大于螺旋位错的结合能这一点研究人员是有共识的。因此，如公式（1）所示，刃型位错四周的氢浓度大于螺旋位错四周的氢浓度，这说明，在体心立方金属中，氢在刃型位错四周可容易形成科特雷尔气氛（Cottrell atmosphere），在刃型位错的芯部，氢的浓度很高。在面心立方晶格的纯镍中，位错和氢间的结合能为8.7～19.3kJ/mol。该结合能级要比体心立方金属低得多，这说明面心立方金属的位错四周的氢浓度要比体心立方金属低得多。例如，有报道说，随体心立方晶格的2.25Cr～1Mo钢的位错密度的增加，氢的扩散速率下降。这说明，在体心立方金属中，氢和位错之间的相互作用大。相反，在面心立方晶格的纯镍中，由于塑性变形，氢的扩散率增加。这说明，面心立方金属的氢和位错之间的相互作用与氢扩散没有多少关系。这些结果表明了体心立方金属位错和氢之间相互作用及面心立方金属位错和氢之间相互作用的差别。

 

下面谈一下运动位错造成的氢传输和应力—应变曲线之间的关系。总体来说，在室温条件下，当塑性变形开始时，各个晶体组织内的刃型位错迁移率大于螺旋位错。因此，高迁移率的刃型位错在滑移线上移动，首先达到试样表面，在接着的塑性变形中，螺旋位错起主要作用。刃型位错和螺旋位错之间迁移率的差别与本研究中所获得的氢解吸光谱相一致。塑性变形开始，氢解吸的急剧增加说明具有大结合能的刃型位错将大量的氢传输到试样表面。在塑性变形开始时，位错密度低，在滑移面上的障碍少，所以，位错可在初始滑移系的滑移面上长距离直线移动。在接着的塑性变形中氢解吸的降低与螺旋位错传输氢的降低相一致。这是由于螺旋位错和氢之间的结合能较小，也就是说，氢在螺旋位错四周的科特雷尔气氛（Cottrell atmosphere）较小。另外，由于其相互作用趋于造成交叉滑移，导致在晶界形成并累积紊乱蜂窝状结构，使试样表面长距离移动的位错数量降低。而且，在接着进行的塑性变形过程中，空位的密度大于塑性变形开始的密度。由于空位是氢和位错的捕获地点，但对氢更加稳定，氢易于捕获在试样中的空位中，因此，运动位错传输的氢的数量会降低。

 

 

4.3运动位错传输的氢和应变速率之间的关系 

 

如公式（1）所示，在没有捕获时晶格内间隙位置氢的释放和氢的存在是随温度增加的。因此位错芯部和弹性应力场四周的部分氢是随温度的上升而下降的。虽然有许多位错在滑移表面上移动并到达试样表面，但是在温度较高时，应变速率对运动位错传输的氢的数量的影响很小，原因就是位错四周氢的浓度很低。相反，在温度较低时，应变速率（平均位错速度）的影响要大得多，这是因为位错四周氢的浓度较高所致。平均位错速度的v表达式如下：

 

v=2ε/ρb ………………………………（2）

 

式中，ε是应变速率，ρ是运动位错的密度，b是伯格斯矢量（burgersvector），当位错速度v和氢的扩散速率相同，或位错速度v稍微大一点时，氢可随运动位错移动，位错和氢之间的相互作用的影响最大。对纯铁来说，当金属在4.2×10－4/s的应变速率进行拉伸变形时，拉伸应力促使的氢解吸的最大数量为0.21ppm， 也就是说，为初始氢含量的16%。该结果表明，在该应变速率时，位错和氢之间的相互作用的影响相当大。在4.2×10－3/s的应变速率时，运动位错传输的氢数量的下降原因是位错速度要比氢扩散速度高得多，也就是说，是4.2×10－4/s的应变速率时的10倍。因此，只有少量的氢与位错相互作用。在4.2×105/s的应变速率时运动位错传输的氢的总量下降的原因是氢的扩散率要比位错速度高得多，也就是说，是4.2×10－5/s的应变速率时的十分之一。因此，在由位错传输前，氢会由于热活化过程自行扩散到试样表面。

 

在室温条件下，Inconel 625的氢扩散系数比纯铁低六个数量级。因此，对Inconel 625来说，在4.2×10－4/s的应变速率时,平均位错速度要比氢扩散速度高得多。人们预计，当应变速率比4.2×10－4/s 的应变速率低三个数量级时，位错和氢之间会产生相互作用。在应变速率为4.2×10－4/s，4.2×10－5/s和4.2×10－6/s时，拉伸应力促使的氢解吸量分别1%、5%和9%，见表2所示。关于应变速率与氢解吸之间相互关系的试验结果完全与预计的位错和氢速度之间的相互作用一致。正如在上一节所讨论的那样，纯铁中运动位错传输的氢的速率（16%）大于Inconel 625的原因有三个：

 

（I）体心立方晶格铁中位错和氢间的结合能要大于面心立方晶格铁。（II）bcc晶格的铁中氢稳定位置是在bcc金属滑移平面（112）四面体位置，氢容易被运动位错阻塞。（III）在纯铁中，位错可长距离运动。在本研究中，使用的是纯铁和Inconel 625，研究结果清楚地表明，氢是由运动位错传输的，这是在氢和应力条件下产生的物理现象。拉伸应力促使的氢解吸并不会直接造成氢脆，但是，就局部区域——如晶界，蜂窝状组织，各种沉淀物和夹杂——内的氢和氢聚集而增强的位错动力造成晶格缺陷的增加而言，它是这种氢脆的重要基本现象之一。由于高强度钢中有许多位错运动的障碍，如位错密度，各种各样的沉淀物和细化晶界，所以还需在氢脆环境中进一步检测氢的解吸行为。

 

 

5、结论

在室温条件下的变形过程中，在现场分析了造成断裂应变的体心立方金属纯铁和面心立方金属Inconel 625的弱捕获扩散氢的解吸行为。有关弹性/塑性变形对氢解吸行为影响的结果总结如下：

 

⑴在拉伸变形过程中，通过从充氢试样释放出来的氢总量中减去吸附的H2O中解吸出来的碎片氢和在室温条件下没有施加应变时释放的H2，就可预测出应力促使的氢解吸行为。

 

⑵在弹性变形时，氢很少解吸。相反，当塑性变形开始，当屈服强度达到最大值时，解吸迅速增加，然后，随着施加的应变增加而逐渐降低。解吸行为可能与塑性变形过程中的运动位错紧密相关，并取决于位错类型，如刃型或螺旋位错和位错运动。

 

⑶在不同的应变速率条件下，拉伸变形过程中的解吸氢总量不同。当氢的扩散系数高的纯铁在应变速率4.2×10－5/s进行变形时，观察了拉伸应力促使的解吸氢总量。它为初始氢含量的16%。在应变速率4.2×10－5/s，4.2×10－3/s时，解吸氢总量下降。相反，对氢的扩散率较低的Inconel 625来说，随着应变速率的下降，解吸氢的总量上升。当Inconel 625在应变速率4.2×10－6/s时，拉伸应力促使的最大氢解吸总量为初始氢含量的9%。氢解吸总量的差别可能是与随运动位错移动的氢总量有关。